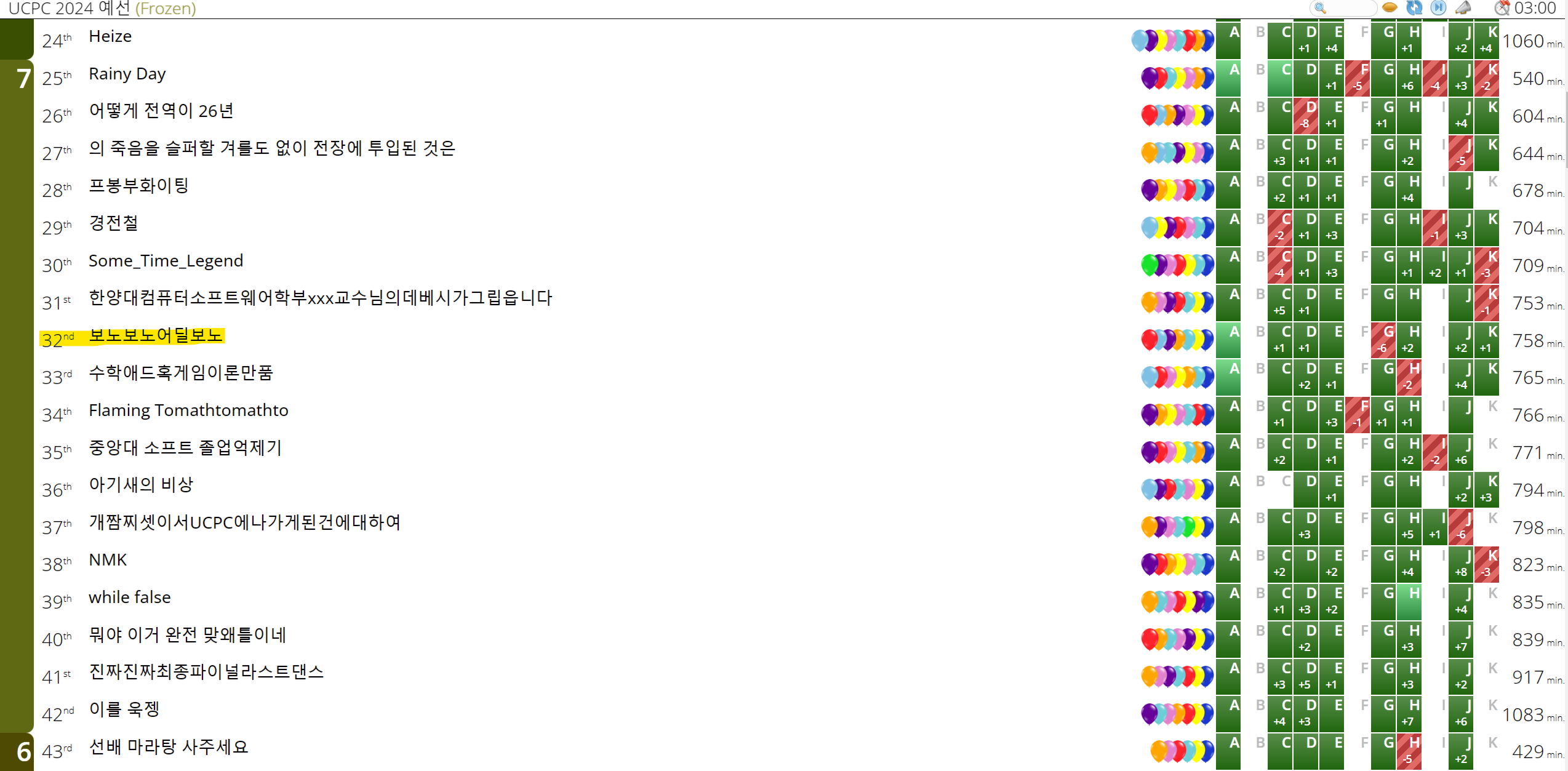
 7솔브로 32등을 하였습니다. 아마 결과가 나와봐야겠지만, 본선에 진출할 수 있을 듯 합니다.
7솔브로 32등을 하였습니다. 아마 결과가 나와봐야겠지만, 본선에 진출할 수 있을 듯 합니다.
+ 본선에 진출하였습니다.
최종 전체 스코어보드 펼치기/접기

문제 정보
대회 시작 전
원래는 ICPC 팀으로 나가려 했으나 jinhan814가 본선 당일 개인 일정이 있어 tmdghks과 같이 나갔습니다. 예선은 저와 eoaud0108은 학교에서 같이 하기로 했고, tmdghks은 다른 장소에서 디스코드를 통해 소통하기로 했습니다.
A가 가장 쉬운 문제임은 이미 공지 되어 있는 상태여서, A는 제가 빠르게 풀기로 했습니다. eoaud0108는 앞부터 차례로 본다고 했고, tmdghks은 쉬운 문제를 찾는다고 한것 같은데, 정확히 기억나지는 않네요.
대회 중
우선 계획대로 A를 봤습니다. 지문은 길어보여서 일단 입출력을 읽었습니다. 입력을 보니 직사각형 모양이 주어지는 것 같고, 출력을 보니 안에 들어가는 원의 최대 반지름을 구하라는 것 같아 예제를 보니 맞아보였습니다. 단위를 굵게 칠해 준 것도 도움이 되었습니다. 보자마자 풀어 코딩에 들어갔습니다.
A번 풀이 펼치기/접기
사용 알고리즘
- 사칙연산(Arithmetic)
$\min(h,w)\times50$을 출력하면 됩니다.
코드
#include<bits/stdc++.h>
using namespace std;
#ifdef kidw0124
constexpr bool ddebug = true;
#else
constexpr bool ddebug = false;
#endif
#define debug if constexpr(ddebug) cout << "[DEBUG] "
void solve(){
int h,w;
cin>>h>>w;
cout<<min(h,w)*50<<'\n';
}
int main() {
#ifdef kidw0124
freopen("input.txt","r",stdin);
freopen("output.txt","w",stdout);
clock_t st=clock();
#else
ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#endif
int t=1;
// cin>>t;
while(t--)solve();
#ifdef kidw0124
debug<<clock()-st<<"ms\n";
#endif
}
이 문제를 풀고 B는 eoaud0108가 보고 있어서 저는 C를 봤습니다. 그림을 보는데 얼마 전 Solved.ac 마라톤에서 본 BOJ 24536 - 정원장어문제와 같은 문제인 줄 알고 제가 잡겠다고 했습니다.
이 사이 tmdghks이 E가 쉬운 문제인 것 같다고 하였고, 동시에 J가 상당히 많은 틀린 제출이 있다는 것을 확인했습니다. eoaud0108이 E를 보더니 그리 쉬운 문제는 아닌 것 같다고 하였고, tmdghks와 eoaud0108이 J는 그리디하게 하면 안되는지, 그렇다면 저렇게 많은 오답 제출이 있을 것 같지 않다고 얘기하며 다른 문제를 보고 있었습니다.
그러는 동안 제가 잡은 C가 기존의 문제와 같은 문제가 아님을 알았고, 스코어보드에 E가 풀린 것을 확인했습니다. 그리고 tmdghks가 E가 브루트포스인 것 같다고 하였고, 저도 브루트포스로 될 것 같아서 풀었습니다.
E번 풀이 펼치기/접기
사용 알고리즘
- 그리디(Greedy)
- 정렬(Sort)
- 브루트포스(Brute Force)
- 시뮬레이션(Simulation)
과제가 $N$개가 있고, 각각 기한이 있습니다. 과제 하나를 하는 데는 $A$만큼 시간이 걸립니다. 실버(문제 주인공)은 딱 한 번 원하는 시각에 원하는 $X(1\le X \le A-1)$를 골라 $BX$ 만큼 자고, 이후 과제를 하나 하는데 걸리는 시간을 $A-X$로 만들 수 있습니다. 과제를 최대한 많이 하는 개수를 구하는 문제입니다.
$N, A, B$의 범위가 $100$이하입니다. 우선 주어진 과제의 마감 기한을 정렬합니다. 과제별 가중치가 없으므로 과제를 끝낼 수 있다면 가능한 앞쪽 과제를 끝내는 것이 이득입니다. 잠에 들기 전 $i$개의 과제를 끝내거나 포기하고, $j$만큼 자고 일어났을 때, 얼마나 많은 과제를 할 수 있을 지 구합니다. $i$와 $j$가 정해지면, 그리디하게 배정하면 되므로 $O(N)$에 $i$, $j$에서 최대값을 구할 수 있습니다. 따라서 $O(N^2A)$에 풀 수 있습니다.
코드
#include<bits/stdc++.h>
using namespace std;
#ifdef kidw0124
constexpr bool ddebug = true;
#else
constexpr bool ddebug = false;
#endif
#define debug if constexpr(ddebug) cout << "[DEBUG] "
void solve(){
int i,j,k;
int n,a,b;
cin>>n>>a>>b;
vector<int>trr(n+1);
for(i=1;i<n+1;i++){
cin>>trr[i];
}
sort(trr.begin(), trr.end());
int ans=0;
for(i=0;i<n;i++){
for(j=0;j<a;j++){
int tmp=0,now=0;
for(k=1;k<=i;k++){
if(now+a<=trr[k]){
now+=a;
tmp++;
}
}
now+=b*j;
for(k=i+1;k<=n;k++){
if(now+(a-j)<=trr[k]){
now+=a-j;
tmp++;
}
}
ans=max(ans,tmp);
}
}
cout<<ans<<'\n';
}
int main() {
#ifdef kidw0124
freopen("input.txt","r",stdin);
freopen("output.txt","w",stdout);
clock_t st=clock();
#else
ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#endif
int t=1;
// cin>>t;
while(t--)solve();
#ifdef kidw0124
debug<<clock()-st<<"ms\n";
#endif
}
E를 구현하는 중 C, D, G, H, J가 풀렸습니다. eoaud0108이 D는 쉬워보인다고 해서 잡기로 했고, tmdghks는 나머지 문제들을 생각하기로 했습니다.
제가 E를 AC를 띄우고 J를 보니 그리디하게 될 것 같아 잡았습니다. 동전이 일렬로 주어질 때 “연속된”, “같은” 두개의 동전을 뒤집어 모두 앞면을 보게 하는 최소 시행을 구하는 것인데, 제가 “연속된”만 보고 “같은”을 보지 않고 제출해 한 번 틀렸습니다.
다시 돌아와서 J가 해당 방식으로 되지 않는 다는 것을 알고 일단 다른 문제를 읽기 시작했습니다. C는 아까 생각해봤었고, D는 eoaud0108가 풀고 있으니, G를 봤습니다. G는 문제는 이해 됐는데, 도저히 머리로 입체가 그려지지 않아 일단 넘어갔고, G에서 머리가 띵해져서 H를 읽기보다 그냥 J를 다시 생각하기로 했습니다.
그 사이 eoaud0108이 D를 풀어 제출했으나, WA를 받았습니다. 단순 세그로 풀린다는데, WA가 왜 떴는 지 모르겠다고 하며 eoaud0108가 D 틀린 것을 찾기로 했고, tmdghks은 G를 그냥 하면 될 것 같다며 G를 풀기로 했습니다.
저는 J를 그리디였으면 다른 팀들이 다 풀었을 텐데, HH를 뒤집어야 하는 예시가 있나 생각하다가 THTTHT라는 기깔난 예시를 찾았습니다. 그리고 이는 재귀적으로 풀리겠다 생각했으나, TLE가 나는 것이 분명해 보여 해당 문제 더 생각이 나지 않아 그냥 아까 C를 생각하던 것이 있어 다시 보기로 했습니다. 나중에 통계를 통해 알게 되었는데, J는 WA보다 TLE가 월등히 많이 제출된 문제였습니다. 그러니까 제가 이 때 “그리디가 아니여서 다른 팀들이 틀렸을거야”라고 생각한 것은 사실 아니였고 다른 팀들은 시뮬레이션처럼 진행해 그랬던 것 같습니다.
이 때 eoaud0108가 D 코드에서 세그를 구성할 때 1<<18의 크기로 구성했고, 이것이 범위가 작아 설마 이것 때문에 틀리나 싶어 다시 제출한다 했는데, 그 설마가 맞았어서 허무하게 D를 맞았습니다.
D - 이진 검색 트리 복원하기 [+1, 0:50:57]
저는 C를 풀고 있고, tmdghks는 G를 풀고 있고, H가 많이 풀려 eoaud0108가 H를 보기로 했습니다. H를 보더니 eoaud0108가 만조분이라고 하며 이를 풀기로 했습니다.
10분 쯤 지나고 eoaud0108가 H를 제출하며 이건 WA 많이 뜰수도 있다고 했습니다. 예상대로 첫 제출은 WA가 떴고 20분 뒤 두 번째 제출도 WA가 떴습니다.
그 사이 저는 C코딩을 끝냈고, 제출했으나 WA가 나왔습니다. L과 R이 나뉘는 지점을 기준으로 모두 돌았는데, WA가 떠서 혹시나 풀이가 틀렸나 열심히 고민하던 중, LR이 안나뉘고 모두 R이거나 모두 L일 수 있음을 깨달아 이를 고쳐 제출하니 AC가 떴습니다. 자세한 설명은 아래에 있습니다.
C번 풀이 펼치기/접기
사용 알고리즘
- 그리디(Greedy)
- 정렬(Sort)
- 브루트포스(Brute Force)
왼쪽 혹은 오른쪽을 보고 있는 미어캣 $N$마리가 있습니다. $N$마리의 미어캣은 서로 다른 위치에 일렬로 서 있고, 키가 서로 다릅니다. 같은 방향을 보고 있는 미어캣들의 순서를 재배치하는 것은 가능합니다. 다만 L과 R의 배치는 유지되어야 합니다. 즉, 서로 다른 방향을 보고 있는 미어캣들의 순서를 바꾸는 것은 불가능합니다.(이것이 정원장어와 다른 점입니다)
최종적으로 각 미어캣에 대해 자신이 바라보는 방향에 자신보다 키가 큰 미어캣이 없는 경우 망을 볼 수 있습니다. 이때 망을 볼 수 있는 미어캣의 최대 수를 구하는 문제입니다.
정원장어의 아이디어를 그대로 갖고 올 수 있습니다. 망을 보는 미어캣은 LL...LLRR...RR의 순서로, L에서는 오름차순 R에서는 내림차순의 키를 가지고 있어야 합니다. RL이 있는 경우 둘 중 키가 작은 미어캣은 다른 미어캣에 막히게 됩니다. 즉, LR의 지점이 최대 $N$개 있을 수 있고, 이를 고정시켰다고 생각해봅니다.
기준점을 기준으로 왼쪽 L의 경우 망을 최대한 봐야 하므로 키가 커야 하며, 오른쪽 L의 경우 최대한 키가 작아야 합니다. 즉, 기준점 바로 옆 L에 가장 키가 큰 것을 놓고, 왼쪽으로 가며 차례로 내림차순으로 키가 작아지도록 배치합니다. 그리고 기준점 오른쪽 R의 경우 최대한 많이 봐야 하므로, 기준점 오른쪽의 L은 오른쪽으로 갈 수록 키가 작아지게 하면 됩니다. 만약 이 경우 R이 L에 막혀 보지 못한다면 L의 순서를 바꾸면 그 R은 계속 못보며 새로운 못보는 것이 생길 수 있으므로 이것이 이득입니다. 정리하자면, 기준점을 기준으로 왼쪽에 가장 키가 큰 L을 놓고, 왼쪽으로 가면서 키가 큰 순서대로 L을 차례로 놓아 준 뒤, 다시 기준점으로 와서 오른쪽으로 가며 키가 큰 순서대로 L을 배치하면 됩니다.(ex> 기준점이 |라면 5678|4321) R은 반대로 배치해 줍니다.
모든 기준점이 $O(N)$개 있고, 각 기준점 별로 그리디하게 배치하면 $O(N)$에 해결할 수 있으므로, 총 시간복잡도 $O(N^2)$에 풀 수 있습니다. 정렬의 시간복잡도는 $O(N\lg N)$이므로, 답보다 작습니다.
이때, RR....RR과 LL....LL의 경우도 고려해주어야 합니다. 구현 상에서 $0$이상 $N$이하로 해주면 됩니다. 이 경우를 고려하지 않아 $0$이상 $N$미만으로 구현해 처음에 WA가 떴습니다.
+ 기여를 보니까 정렬 안하고 투포인터로 풀 수 있는 듯 합니다.
+ 정렬을 안하고 투포인터가 아니라 정렬 후 선형 시간에 풀 수 있다는 것 이라고 합니다.
코드
#include<bits/stdc++.h>
#pragma comment(linker, "/STACK:336777216")
#pragma GCC optimize("O3,unroll-loops")
#pragma GCC target("avx,avx2,fma")
using namespace std;
#ifdef kidw0124
constexpr bool ddebug = true;
#else
constexpr bool ddebug = false;
#endif
#define debug if constexpr(ddebug) cout << "[DEBUG] "
void solve(){
int i,j,k;
int n,a,b;
cin>>n;
vector<pair<int,int>> loc(n);
vector<int> lef,rig;
for(i=0;i<n;i++){
cin>>loc[i].first;
char dir;
cin>>dir;
if(dir=='L')lef.push_back(loc[i].first),loc[i].second=0;
else rig.push_back(loc[i].first),loc[i].second=1;
}
if(lef.empty()||rig.empty()){
cout<<n<<'\n';
return;
}
sort(lef.begin(), lef.end());
sort(rig.begin(), rig.end());
int ans=0;
for(i=-1;i<n;i++){
vector<int> tmp(n);
int nowl=lef.size()-1,nowr=rig.size()-1;
for(j=i;j>=0;j--){
if(loc[j].second==0){
tmp[j]=lef[nowl--];
}
}
for(j=i+1;j<n;j++){
if(loc[j].second==1){
tmp[j]=rig[nowr--];
}
}
for(j=i;j>=0;j--){
if(loc[j].second==1){
tmp[j]=rig[nowr--];
}
}
for(j=i+1;j<n;j++){
if(loc[j].second==0){
tmp[j]=lef[nowl--];
}
}
int now=0;
vector<int>maxlef(n),maxrig(n);
maxlef[0]=tmp[0];
for(j=1;j<n;j++){
maxlef[j]=max(maxlef[j-1],tmp[j]);
}
maxrig[n-1]=tmp[n-1];
for(j=n-2;j>=0;j--){
maxrig[j]=max(maxrig[j+1],tmp[j]);
}
for(j=0;j<n;j++){
if(loc[j].second==0){
if(j==0||tmp[j]>maxlef[j-1]) now++;
}
else{
if(j==n-1||tmp[j]>maxrig[j+1]) now++;
}
}
ans=max(ans,now);
}
cout<<ans<<'\n';
}
int main() {
#ifdef kidw0124
freopen("input.txt","r",stdin);
freopen("output.txt","w",stdout);
clock_t st=clock();
#else
ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#endif
int t=1;
// cin>>t;
while(t--)solve();
#ifdef kidw0124
debug<<clock()-st<<"ms\n";
#endif
}
이걸 풀고 나서 eoaud0108가 혹시 H에서 자기가 빼먹은 케이스가 있는 지 확인해 달라고 하며 저에게 문제를 설명하고 케이스들을 설명하고 고민하는 과정에서 하나의 케이스가 더 있음을 발견했습니다. 이를 풀어서 제출하니 AC가 떴습니다.
H번 풀이 펼치기/접기
사용 알고리즘
- 정렬(Sort)
- 많은 조건 분기(Case-Work)
- 애드 혹(Ad-Hoc)
부호가 같은 보관함은 가장 원점에서 먼 보관함만 보면 됩니다.
- 부호가 모두 같다면 가장 먼걸 집고 $D$만큼 이동했다가 오면 됩니다.
- 부호가 다른 것이 있다면, 가장 작은 것(음수)와 가장 먼 것을 보고 아래 중 최소를 택합니다.
- 부호가 같을 때의 행위를 두 번 합니다.
- 한쪽을 집고 와서 반대쪽에서 부호가 같을 때의 행위를 하고, 처음 집었던 것을 놓고 옵니다.
- 만약 둘 사이 거리가 $D$보다
- 크다면, 하나를 집고 반대로 갔다가 다시 놓고 다시 반대로 갔다가 옵니다
- 작다면, 하나를 집고 반대를 가서 집고 처음 집었던 것의 남은 거리를 움직이고 다시 순서대로 놓고 옵니다.
이 경우를 모두 봐 최소를 출력합니다. 정렬을 하거나 최소/최대를 찾아야 하므로 $O(N\lg N)$ 혹은 $O(N)$에 풀 수 있습니다. 범위가 int를 넘어갈 수 있으므로 long long으로 처리해야 합니다.
코드
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
#ifdef kidw0124
constexpr bool ddebug = true;
#else
constexpr bool ddebug = false;
#endif
#define debug if constexpr(ddebug) cout << "[DEBUG] "
void solve(){
int i,j,k;
int n,d;
cin>>n>>d;
vector<ll> arr(n);
for(ll &x:arr)cin>>x;
sort(arr.begin(),arr.end());
if(arr.front()*arr.back()>=0){
cout<<max(abs(arr.front()),abs(arr.back()))*2+d<<'\n';
}
else{
cout<<min({
-arr.front()*2+arr.back()*2+d*2,
-arr.front()*4+arr.back()*2+d*1,
-arr.front()*2+arr.back()*4+d*1,
(arr.back()-arr.front())*2>=d?
(arr.back()-arr.front())*4:
-arr.front()*2+arr.back()*2+d,
})<<'\n';
}
}
int main() {
#ifdef kidw0124
freopen("input.txt","r",stdin);
freopen("output.txt","w",stdout);
clock_t st=clock();
#else
ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#endif
int t=1;
// cin>>t;
while(t--)solve();
#ifdef kidw0124
debug<<clock()-st<<"ms\n";
#endif
}
이제 남은 문제는 B, F, G, I, J, K였습니다. G는 tmdghks이 보고 있고, 솔브 수를 보니 반드시 J를 풀어야겠다고 생각했습니다. 제가 J를 아까부터 보고 있었어서 J를 보고, eoaud0108이 남은 문제를 읽고 생각하고 있었습니다.
그러다가 tmdghks이 G 케이스가 $81$가지인데, 정리하는 것 좀 도와달라고 해 eoaud0108이 도와주기로 했습니다.
저는 J에서 어떤 T를 발견하면 다음 연속된 TT혹은 HH를 뒤집어야 겠다 생각했습니다. 더불어 그렇다면 사이에 반복되어 있을 것이며, THTHTHTHTHTT를 뒤집게 되면 하나씩 밀려 결국 HHTHTHTHTHTH가 됨을 알았습니다. 그래서 연속된 구간을 set에 저장해두고, 앞에서 부터 T를 만나면 다음 구간에서 뒤집고, 길이만큼 더한 뒤 다시 넣는 방식으로 반복하는 코드를 작성해 제출했으나 WA가 나왔습니다. 나중에 풀이를 알고 보니 해당 set을 depth마다 만들면 정해의 stack에서 size랑 대응되어 동치인 풀이가 나온다는 것을 알게 되었습니다.
일단 WA가 나온 시점에서 저는 J에서 아이디어를 떠올리기 힘들다고 생각을 했고, 아까 나온 “재귀”의 아이디어를 분할정복으로 바꾸어 풀 수 있을 지 고민했습니다. 그래서 대충 생각했으나 THHHT가 NO가 나온다는 것을 알고, 가능/불가능 판정이 해당 방식으로는 어려울 것 같아 해당 방식은 버리게 되었습니다. 이 시점에서 J는 제 문제가 아닌가보다 하고 eoaud0108에게 넘기기로 하였습니다.
남은 B, F, I, K 중 B, F, I는 지문 읽으면서 어려운 스멜이 났고, K는 그나마 구성적이여서 할만해 보였습니다. 실제로 스코어보드도 G, J를 제외하면 K처럼 보여 K를 잡기로 했습니다. eoaud0108가 읽었어서 문제를 설명해주었고, 저는 다른 제한보다 $A+B$가 변의 길이 이하라는 제한에 집중해보기로 했습니다.
우선 홀수 차수가 홀수 개면 안되는 것은 자명했고, 일렬로 쭉 나열한 것을 생각해보니 홀수가 $2$개 있는 경우는 항상 가능함을 알 수 있었습니다. 더 나아가 홀수가 $2$개 이상일 때는 반드시 만드는 경우가 있음을 알았고, 남은 경우는 홀수가 $0$개 있을 때 짝수가 문제였습니다. 자세한 설명은 아래 풀이에 적어두었습니다.
대충 이 시점에서 스코어보드는 프리즈 되었습니다.

프리즈 시점 전체 스코어보드 펼치기/접기

프리즈 시점에 5솔 1등으로 42등이였기 때문에, 패널티는 저희 팀도 관리를 잘 못했지만, 전체적으로 관리가 어렵다는 판단을 했고, 못해도 1솔브는 더, 웬만하면 2솔브는 더 풀어야겠다고 생각했습니다. G번의 경우 맞는 것을 바라는 것은 너무 도박일 수 있었기 때문에, J와 K를 푸는 것을 목표로 했습니다. K는 거의 풀렷다고 생각했기 때문에 이 시점에서 tmdghks에게 부담을 가지지 말라고 했고, G는 맞으면 좋다의 마인드로 접근했습니다.
그리고 조금 더 생각하다가 K에서 가능한 경우들을 찾아 풀었습니다.
K번 풀이 펼치기/접기
사용 알고리즘
- 구성적(Constructive)
- 많은 조건 분기(Case-Work)
- 애드 혹(Ad-hoc)
우선 홀수가 $2$개 이상 있다면 아래와 같이 배치할 수 있습니다. 우선 양 끝에 홀수 차수 점 $2$개를 배치한 다음 남는 홀수 차수는 짝수개 이므로, 지그재그로 배치합니다. 그리고 짝수들에 대해서는 차수가 2가 되도록 일렬로 배치해주면 됩니다.
.O.O.O.......
OOOOOOOOOOOOO
..O.O.O......
K에서 홀수가 $0$개 있을 때 짝수를 몇개 채우는 것을 고민해봤습니다. 우선 ㅁ모양으로 채우면 4개가 가능하며, 예제처럼 ㅁ에 끝 모서리에 $3$개씩 더해가면 $3k+1$꼴이 된다는 것을 알았습니다. 덤으로 ㅁ도 점 하나에서 $3$개를 더했다고 생각했습니다.
O OO OO OO
OO OOO OOO
OO OOO
OO
또한 $8$, $12$일 때 아래 모양 처럼됨을 알았습니다. 나중에 알았는데 $8$은 예제에 있었습니다. 이거에서 $3$개씩은 붙여나갈 수 있으므로 8이상의 $3k+2$, 12이상의 $3k$꼴은 모두 됨을 알 수 있습니다.
OOO OOOO OOO
O.O O..O O.O
OOO O..O OOOO
OOOO OO
추가로, 이걸 짜고 제출 후에 생각난 방식으로 아래와 같이 $8$이상의 짝수를 모두 만들 수도 있습니다. 또한 오른쪽 아래에 3개를 붙이는 방식으로 $11$이상의 홀수도 모두 만들 수 있습니다.
OOO OOOO OOOOO
O.O O..O O...O
OOO OOOO OOOOO
남는 수는 $2$, $3$, $5$, $6$, $9$인데, $9$는 예제에 안된다고 주어져 있고, 나머지는 아무리 해봐도 안되길래 확신의 믿음을 가지고 제출했습니다.
그러나 WA가 나오길래 아무리 봐도 맞는데 구현 실수인가 하다가 YES인 경우에 YES와 행과 열의 크기를 출력하지 않았음을 알아 다시 제출해 AC를 띄웠습니다. 시간복잡도는 유의미하지 않지만 $O(N^2+A+B)$입니다. $N$은 $200$으로 고정했습니다.
코드1(대회 중에 낸 방식)
#include<bits/stdc++.h>
using namespace std;
#ifdef kidw0124
constexpr bool ddebug = true;
#else
constexpr bool ddebug = false;
#endif
#define debug if constexpr(ddebug) cout << "[DEBUG] "
void solve(){
int i,j,k;
int n,m;
cin>>n>>m;
vector<string> arr(200,string(200,'.'));
if(m==0){
if(n%3==1){
arr[0][0]='O';
i=1;
for(j=0;j<(n-1)/3;j++){
arr[i][i-1]='O';
arr[i][i]='O';
arr[i-1][i]='O';
i++;
}
}
else if(n%3==2){
if(n<8){
cout<<"NO\n";
return;
}
arr[0][0]=arr[0][1]=arr[0][2]
=arr[1][0] =arr[1][2]
=arr[2][0]=arr[2][1]=arr[2][2]='O';
i=3;
for(j=0;j<(n-8)/3;j++){
arr[i][i-1]='O';
arr[i][i]='O';
arr[i-1][i]='O';
i++;
}
}
else{
if(n<12){
cout<<"NO\n";
return;
}
arr[0][0]=arr[0][1]=arr[0][2]=arr[0][3]
=arr[1][0] =arr[1][3]
=arr[2][0] =arr[2][3]
=arr[3][0]=arr[3][1]=arr[3][2]=arr[3][3]='O';
i=4;
for(j=0;j<(n-12)/3;j++){
arr[i][i-1]='O';
arr[i][i]='O';
arr[i-1][i]='O';
i++;
}
}
}
else if(m&1){
cout<<"NO\n";
return;
}
else{
arr[0][2]='O';
i=1;
for(j=0;j<(m-1)/2;j++){
arr[i][2]='O';
if(j&1){
arr[i][1]='O';
}
else{
arr[i][3]='O';
}
i++;
}
for(j=0;j<n;j++){
arr[i][2]='O';
i++;
}
arr[i][2]='O';
}
cout<<"YES\n";
cout<<"200 200\n";
for(i=0;i<200;i++) {
cout << arr[i] << '\n';
}
}
int main() {
#ifdef kidw0124
freopen("input.txt","r",stdin);
freopen("output.txt","w",stdout);
clock_t st=clock();
#else
ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#endif
int t=1;
// cin>>t;
while(t--)solve();
#ifdef kidw0124
debug<<clock()-st<<"ms\n";
#endif
}
코드2(제출 후 생각한 더 조건이 적은 방식)
#include<bits/stdc++.h>
using namespace std;
#ifdef kidw0124
constexpr bool ddebug = true;
#else
constexpr bool ddebug = false;
#endif
#define debug if constexpr(ddebug) cout << "[DEBUG] "
void solve(){
int i,j,k;
int n,m;
cin>>n>>m;
vector<string> arr(200,string(200,'.'));
if(m==0){
if(n%3==1){
arr[0][0]='O';
i=1;
for(j=0;j<(n-1)/3;j++){
arr[i][i-1]='O';
arr[i][i]='O';
arr[i-1][i]='O';
i++;
}
}
else{
if(n%2==1&&n<11){
cout<<"NO\n";
return;
}
if(n<8){
cout<<"NO\n";
return;
}
int x=n%2;
if(x)n-=3;
for(i=0;i<(n-2)/2;i++){
arr[i][0]=arr[i][2]='O';
}
arr[0][1]='O';
arr[i-1][1]='O';
if(x){
arr[i][2]=arr[i][3]=arr[i-1][3]='O';
}
}
}
else if(m&1){
cout<<"NO\n";
return;
}
else{
arr[0][2]='O';
i=1;
for(j=0;j<(m-1)/2;j++){
arr[i][2]='O';
if(j&1){
arr[i][1]='O';
}
else{
arr[i][3]='O';
}
i++;
}
for(j=0;j<n;j++){
arr[i][2]='O';
i++;
}
arr[i][2]='O';
}
cout<<"YES\n";
cout<<"200 200\n";
for(i=0;i<200;i++) {
cout << arr[i] << '\n';
}
}
int main() {
#ifdef kidw0124
freopen("input.txt","r",stdin);
freopen("output.txt","w",stdout);
clock_t st=clock();
#else
ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#endif
int t=1;
// cin>>t;
while(t--)solve();
#ifdef kidw0124
debug<<clock()-st<<"ms\n";
#endif
}
이걸 짜는 동시에 eoaud0108가 J풀이를 찾아 구현해 AC를 받았습니다.
J번 풀이 펼치기/접기
사용 알고리즘
- 스택(Stack)
- 그리디(Greedy)
- 애드 혹(Ad-hoc)
우선 T를 발견했을 때, 뒤에 HH를 가져오게 되면 HH가 HT가 됩니다. 즉, 이는 또다른 T와 만나야 하므로, 사이에 짝수개가 있는(이렇게 되면 홀짝성에 의해 가운데에 HH가 반드시 존재합니다) 다음 T를 발견하는 것이 중요합니다. 즉, 사이에 짝수개인, 인덱스 차이가 홀수인 T를 발견하면 스택에서 뽑고 아니면 스택에 넣는 것을 하여 최종적으로 스택이 비어있는 지를 검사하면 됩니다. $O(N)$에 풀립니다. 이는 결국 set풀이에서 depth를 준 것과 동치입니다. 답이 int범위를 넘어갈 수 있으므로 long long을 사용했습니다.
코드
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
#ifdef kidw0124
constexpr bool ddebug = true;
#else
constexpr bool ddebug = false;
#endif
#define debug if constexpr(ddebug) cout << "[DEBUG] "
void solve(){
int i,j,k;
int n;
cin>>n;
string str;
cin>>str;
stack<int>stk;
ll ans=0;
for(i=0;i<n;i++){
if(str[i]=='T'){
if(stk.empty() || (stk.top()-i)%2==0){
stk.push(i);
}
else{
ans+=i-stk.top();
stk.pop();
}
}
}
if(stk.size())cout<<"-1\n";
else cout<<ans<<'\n';
}
int main() {
#ifdef kidw0124
freopen("input.txt","r",stdin);
freopen("output.txt","w",stdout);
clock_t st=clock();
#else
ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#endif
int t=1;
cin>>t;
while(t--)solve();
#ifdef kidw0124
debug<<clock()-st<<"ms\n";
#endif
}
이후 마지막 1분을 남기고 tmdghks이 G를 짜 제출했으나 틀렸습니다.
대회 후 총평
개인적인 피드백
우선 J에서 틀린 풀이는 어쩔 수 없다 쳐도, C에서 끝을 탐색하지 않은 것, 그리고 K에서 말도 안되는 출력을 안한 것으로 패널티를 쌓은 것은 정말 하면 안되었던 것 같습니다. 대회 초반 E나 C구현할 때 엄청 머리 아프고 집중이 되지 않았었는데, 다음부터는 대회 전에 일찍 일어나 머리를 풀어 두어야 하겠습니다.
팀 피드백
오늘은 tmdghks가 온라인으로 같이 해 소통을 잘 하지 못했지만, 본선 때 잘 해보도록 하겠습니다.
]]>
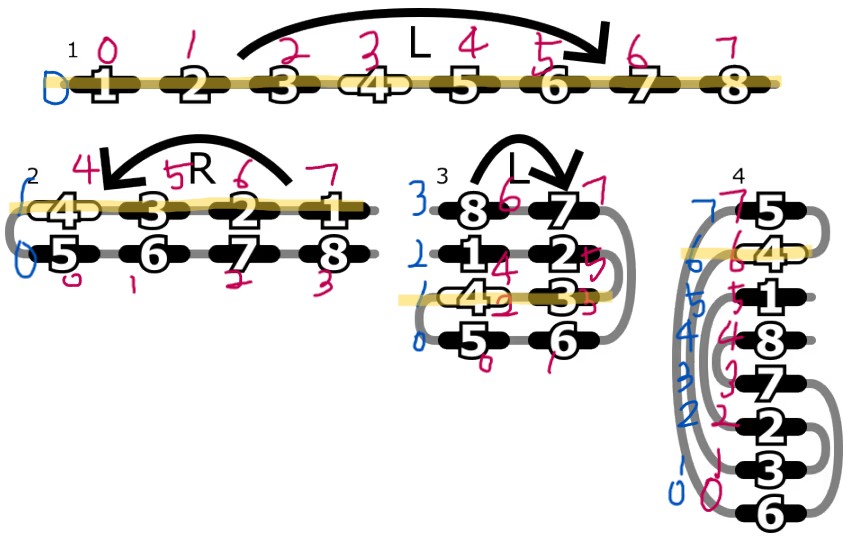 이제 최종 마지막 상태에서 역으로 생각해 보면 다음을 알 수 있습니다.
이제 최종 마지막 상태에서 역으로 생각해 보면 다음을 알 수 있습니다.